Advanced Optimization Strategies for Accelerated Materials Discovery

Novel functional materials are at the core of next-generation energy and environmental technologies, consumer products, food and water safety, healthcare, etc. With the rapidly developing materials fabrication and characterization capability comes the need to answer the question: Which material designs exhibit optimal material functionality?. The traditional experimental trial-and-error approach is expensive and not on par with the near-atomic precision of new experimental technologies and the vast design space of potential material candidates. Thus computational materials discovery has been gaining increasing research interest.

Generally, computational materials discovery consists of four major components: structure generation, structure representation, properties calculation, and structure optimization. Researchers have traditionally focused on the former three components, with many exciting advancements utilizing artificial intelligence technologies. For example, using generative models to generate stable structures, representing structures with learned embeddings, and predicting materials properties with efficient and accurate NN models. On the contrary, structure optimization hasn’t been extensively studied in the literature, despite that it is at the core of computational materials discovery.

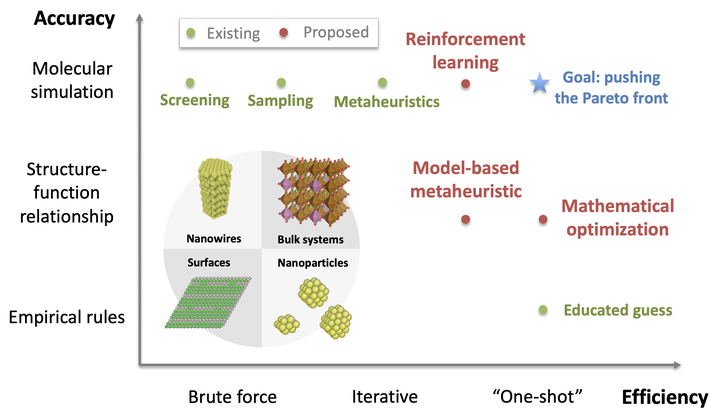
We have focused on developing advanced optimization strategies for accelerated materials discovery in the past few years. The main research goal is to push the accuracy-efficiency Pareto front (see above) to high accuracy and high-efficiency region. Various approaches have been proposed, including mathematical optimization, model-based metaheuristic, and reinforcement learning approaches. More recently, other important aspects, such as scalability, generalizability, and interpretability, have also been investigated.

Designing semiconductor nanowires with mathematical optimization

• Represent materials using arrangements of building blocks and introduce integer decision variables
• Cast (simplified) structure-function relationships into mathematical optimization programs
• Solve optimization programs with optimization techniques/solvers commonly used in the PSE community

MatOpt: materials design via mathematical optimization

• To provide a building blocks-based materials representation system
• To provide a simplified modeling interface that does not require details of mathematical optimization concepts
• To automate the workflow of carrying out materials structure optimization

Designing bimetallic nanoclusters with model-based metaheuristic

• The 3D non-periodic nature and combinatorial complexity make the “one-shot” mathematical optimization intractable
• Proposed customized decomposition algorithms, and combining metaheuristics with mathematical optimization
• Math programs improve search efficiency, and metaheuristics bring solution robustness and time effectiveness

Designing oxide dopants with reinforcement learning

• Learn optimal design heuristics (i.e., policy) instead of pre-defined suboptimal heuristics
• Policy-based design paradigm shows advantages in terms of efficiency, scalability, and generalizability
• Developed software package to cast generic dopants design problem into RL problem